
Circle the date! It's Pi Day today!
Happy Pi Day, the annual celebration of this incredible, mysterious, and irrational mathematical constant.
Happy Pi Day, the annual celebration of this incredible, mysterious, and irrational mathematical constant.
Okay, so Pi — most commonly written as the Greek symbol π — is an essential mathematical constant, equal to 3.14, or 3.1415926, or 3.1415926535897932384626433832795, depending on what kind of calculator you use. However, it goes on for much, much longer.
We use this constant in calculations of geometry and trigonometry, mainly having to do with circles and ellipses and so forth.
By extension, it shows up in many of the sciences, especially in physics and astronomy. Given how weather behaves on our spherical, rotating planet, with the Coriolis effect dominating the motion and behaviour of large storms and weather systems, pi is crucial for all calculations in meteorology.
What is π, really?
Simply enough, pi is the ratio of a circle's circumference to its diameter.
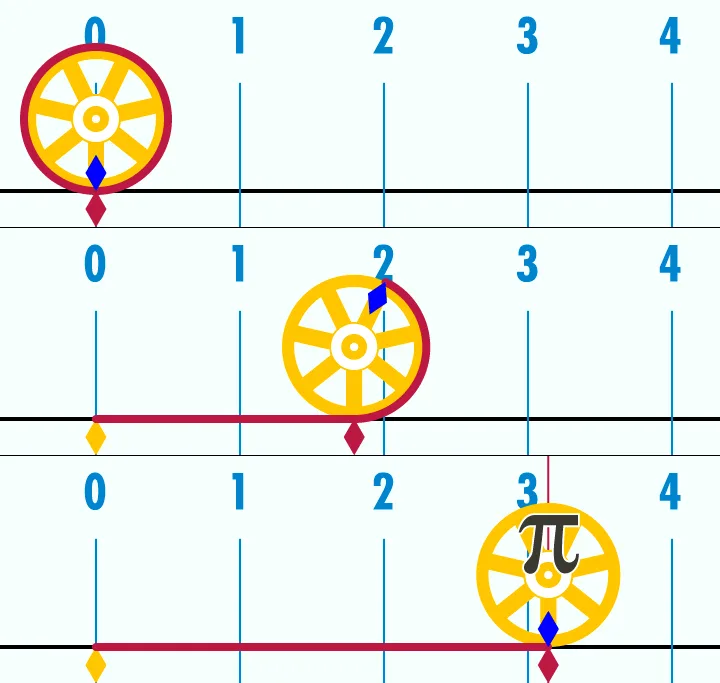
The circumference of a circle rolled out flat plots the value of pi. Credit: Wikimedia Commons
Draw a circle 1 metre across, and its circumference will be pi metres. A circle 1 centimetre across will be pi centimetres around.
Ok, but what makes π so special?
As the above circle unrolls and its circumference is compared to a ruler laid on the ground, the end of the circle will not fall exactly on one of the ruler's marks.
In fact, no matter how close together those marks are, or how small of a space they measure, or how closely we zoom in on the ruler, the end of the circle will never, ever fall exactly on one of the lines.
For this reason, pi is called an irrational number.
What that means is that no matter what you do, you can't divide one whole number by another whole number and arrive at pi. There are examples that come close (such as 22 ÷ 7 = 3.14285714286), but they only give you a rough approximation.
As far as we can tell, given our current level of technology and knowledge of the universe, the decimal places of pi apparently go on forever and produce no pattern of any kind that we can recognize!
Up until the 1400s, the greatest number of digits known for pi was 6 or 7, as computed by Chinese astronomers. Afterwards, approximations and calculation methods became better, and by 1949 we knew of over 1,000 digits. From there, it all came down to computing power. By 1973, they had cracked the first 1 million digits. In 1981 we reached 2 million digits, in 1988 they'd gotten to 200 million digits, and a year later it was up to over 1 billion digits.
As supercomputers became faster and faster, they topped 1.2 trillion digits in 2002, 10 trillion digits by 2011, and Google took that up to 100 trillion in 2022! That number was matched the following year, but taking a little over one-third of the amount of time (59 days instead of the 158 days the 2022 calculation took).
As of today, March 14, 2024, π has been calculated to 105 trillion decimal places.

Even with these incredible computational feats, we still haven't found the end of pi. That's why asking a computer or robot to compute the last digit of pi was such a good trick to use in science fiction stories. If the computer or robot didn't overload in the process, it at least bought the heroes some time to escape.
Perhaps if we were able to look at our universe from the outside, we'd be able to see pi resolve down to a simple, rational number. From here, inside the universe, this mathematical constant holds as an enigma of the cosmos.
Fortunately, the cosmos is forgiving enough that we don't need to know pi to the last digit to produce practical results.
Watch below: The fine people at YouTube's Numberphile channel show how to calculate pi using pies.
π in weather?
How often do we see π show up in meteorology? More often than you might think!
While there aren't too many exact circles in weather, whenever you have rotation — convection, turbulence, storms, supercells and tornadoes, extra-tropical cyclones, tropical storms and hurricanes — pi plays a vital role in that motion!
Take the example of the 'Fibonacci Spiral' pattern produced by the storm that passed over the United States and Canada back on March 11, 2019.
The "Golden Spiral" overlaid onto the storm pattern is one where the radius of the spiral increases so that it matches a Fibonacci number sequence. The sizes of the boxes that the spiral curves through are 1x1, 1x1, 2x2, 3x3, 5x5, 8x8, 13x13 and 21x21, and it would continue with 34x34, 55x55, 89x89, 144x144, etc.
The radius at any point along the curve, though, can be found with the equation below,
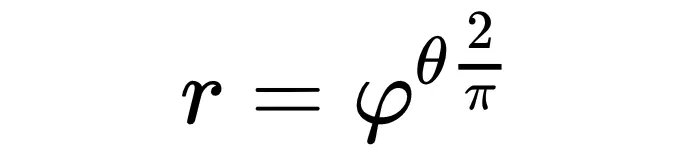
where phi (φ) is the 'golden ratio' (itself an irrational number equal to 1.6180339887...), theta (θ) is the angle from the origin (in radians), and we can see pi figuring prominently in the exponent of the equation.
Frankly, we just can't get away from pi in weather!
Celebrating a mathematical constant?
Conveniently, the name of this particular mathematical constant happens to be a homonym for a delicious dessert treat — pie! Apple pie, cherry pie, blueberry pie, strawberry-rhubarb pie, and even pizza pie.

Pi pie, courtesy koka_sexton/Flickr
As long as it's round, it will do just fine.
Other special constant days
Do we celebrate any other scientific or mathematical constants? Indeed, we do!
There's Pi Approximation Day, on July 22, since 22/7 is a fraction used to approximate pi (it comes out as exactly 3.14285714286).
Depending on whether you write your dates day first or month first, e-Day is on either on January 27 or February 7. It recognizes Euler's Constant, e, which is approximately 2.71 (but it goes on forever, like pi). Calculating compound interest may be its most famous application.
For the chemists, there's Mole Day. A "mole" is a standard measurement of any substance in chemistry, equal to 6.02 x 10²³ atoms or molecules of that substance. As a result, Mole Day is observed on October 23 (10.23), specifically between 6:02 a.m. and 6:02 p.m.
Then there's Tau Day, on June 28, which celebrates the mathematical and scientific constant tau (τ), which is equal to 2 times pi (2π = 6.28571428571...). Or, pi is equal to one half of tau, depending on which side of the rivalry you're on... and yes, there is a rivalry!
Why? Because a circle is defined as the set of all points in a plane that are at a given distance from the centre point. In other words, a circle is defined by its radius, not its diameter. Therefore, to compute the circumference of a circle, you measure from the centre to the edge, and then multiply that number by 2π, or τ. So, the argument is that tau is technically a better mathematical constant than pi.
Unfortunately, while tau may be better, mathematically, it does not have a tasty food associated with it.
For more on pi, and to try out some cool uses of it, check out NASA's Pi in the Sky Challenge!
Thumbnail image shows the Greek symbol for Pi superimposed upon 6600 digits of the mathematical constant
